上章講完prioritized遇到的挑戰跟解決方案，這章節就開始講實作囉！

SumTree

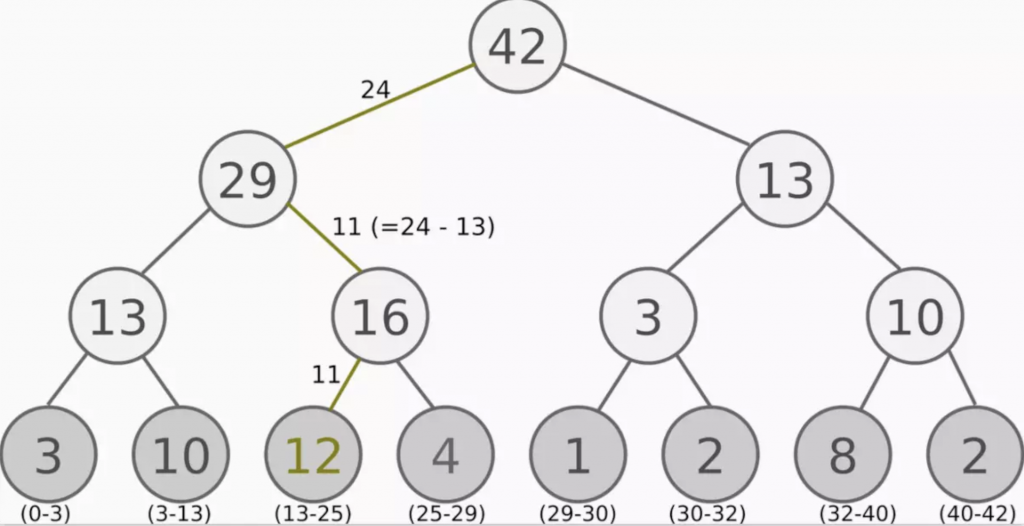
SumTree是種二元節點儲存方式，從上的根節點直到下面底部的節點，節點的值都是由下方的值網上組起來的。我們先來描述如何從樹的結構去找尋想要的值過程：

1. 欲從輸入的值找到放置的節點，先輸入個值。
2. 由最上面節點開始，pointer會先指向根(root node)
3. 往下開始搜尋，抽出下面左右節點做比較。
   1. 如果pointer值沒有比左節點大，則pointer則換成左方節點。
   2. 反之沒有的話，pointer則指向右邊節點，同時pointer會減去左方節點的值
4. 重複3，直到走到最下層，也確定找到了底部節點。
   

程式碼實作

類別初始化。

def __init__(self,capacity):
    self.capacity = capacity
    self.data_pointer = 0
    self.tree = np.zeros(2 * capacity - 1)
    self.data = np.zeros(capacity,dtype=object)
@property
def total_p(self):
    return self.tree[0]  # the root

新增節點的順序是從0開始更新，直至終點再從0開始。

def add(self,p,data):
    tree_idx = self.data_pointer + self.capacity - 1 # 節點index
    self.data[self.data_pointer] = data # 底部index賦予值
    self.update(tree_idx,p)

    self.data_pointer += 1
    if self.data_pointer >= self.capacity:  # replace when exceed the capacity
        self.data_pointer = 0

之前提過上面節點的value都是基於最下面的節點，所以一旦有新的值更新，上面的父節點也會對差值做出改變。

def update(self,tree_idx,p):
    change = p - self.tree[tree_idx]
    self.tree[tree_idx] = p

    while tree_idx!=0:
        tree_idx = (tree_idx - 1) // 2
        self.tree[tree_idx] += change

最後這邊要實作從頭開始找值的方法。

def get_leaf(self,v):
    parent_idx = 0
    while True:
        cl_idx = 2 * parent_idx + 1
        cr_idx = cl_idx + 1
        if cl_idx >= len(self.tree):
            leaf_idx = parent_idx
            break
        else:
            if v <= self.tree[cl_idx]:
                parent_idx = cl_idx
            else:
                v -= self.tree[cl_idx]
                parent_idx = cr_idx
    data_idx = leaf_idx - self.capacity + 1
    return leaf_idx,self.tree[leaf_idx],self.data[data_idx]

結語

樹狀結構根找值我們介紹到這邊，下章接著講怎跟整個訓練做配合的，我們明天見拉～

補充參考

莫凡RL程式碼參考：https://bre.is/tCA5GuPc